회귀 분석 - (3) Partial Regression

partial regression은 각 독립 변수가 종속 변수에 미치는 영향을 파악하는 방법 중 하나다.

$y$에 대해 $x_1$이라는 독립 변수만으로 회귀 분석한 결과가 나온 상황에서, $x_2$라는 새로운 독립 변수를 추가하게 된다면 기존의 $x_1$에 할당된 $w_1$ 가중치의 값이 변하게 될까?

\[y = w_1 x_1 + e\] \[y = w_1 x_1 + w_2 x_2 + e\]

결과를 말하자면, 조건에 따라 다르다.

일반적으로는 $x_1$만으로 회귀 분석을 한 가중치 값과 새로운 변수를 추가한 가중치 값은 다르다. 하지만 다음 두 조건 중 하나를 만족하게 된다면 $w_1$가중치는 두 모델이 동일하다.

1. 독립 변수 $x_2$로 이루어진 특징 행렬 $X_2$와 $y$의 상관관계가 없는 경우
2. 독립 변수 $x_1$과 $x_2$가 상관관계가 없는 경우

Partial Regression Plot

이처럼 종속변수에 대한 각 독립변수 하나의 영향력이 궁금한 경우가 있는데, partial regression plot은 하나의 독립 변수가 종속변수에 끼치는 영향을 시각화한다. statsmodels는 다음과 같은 메소드를 지원한다.

from sklearn.datasets import load_boston
boston = load_boston()
dfX0 = pd.DataFrame(boston.data, columns=boston.feature_names)
dfX = sm.add_constant(dfX0)
dfy = pd.DataFrame(boston.target, columns=["MEDV"])
df = pd.concat([dfX, dfy], axis=1)
model_boston = sm.OLS(dfy, dfX)
result_boston = model_boston.fit()
fig = sm.graphics.plot_regress_exog(result_boston, "CRIM", fig=plt.figure(figsize=(10, 5)))
plt.show()

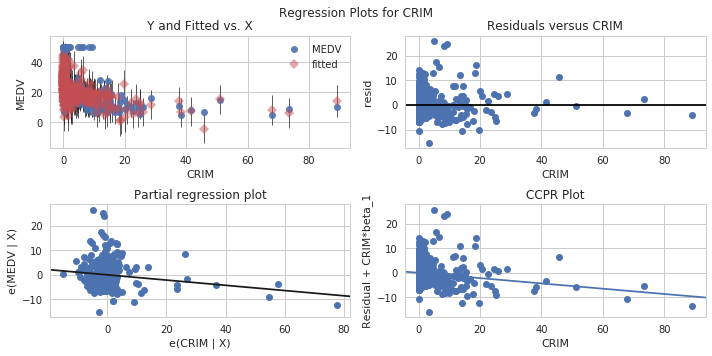
위 그림은 보스톤 집값에 대한 데이터로 partial plot이 포함된 분석 결과를 표현한 것이다.

Y축은 집 값, X축은 범죄율을 의미한다. partial plot만 두고 봤을 때, 범죄율이 높아질수록 집 값을 의미하는 y축의 값이 내려가는 것을 분명히 확인할 수 있다. 하지만 기울기의 크기를 가지고 변수 간의 중요도 비교를 하기에는 적절하지 않(을 것 같)다(비록 스케일링을 했다 하더라도).

References

데이터 사이언스 스쿨 - partial regression