다중 분류 문제 성능평가 [ROC 곡선과 AUC]

이번 포스트에서는 ROC 곡선과 AUC에 대해 정리합니다.
다중분류문제 성능평가 [기본편]에서 이어집니다.

Photo by Markus Spiske on Unsplash

ROC

세상에 있는 도둑을 싹 다 잡으려다보면 억울한 사람도 종종 생기게 될 겁니다. 용의자가 도둑인지 아닌지 구분할 때, (0이면 완전 무죄, 1이면 완전 유죄인 경우) 0.7에 유죄판정을 내릴수도 있고, 0.4에 유죄 판정을 내릴 수도 있는데, 저 0과 1사이의 값을 임계치(threshold)라 합니다. 임계치보다 높은 값은 유죄라고 판단할 때, 이 임계치가 낮으면 조금의 의심만으로도 유죄일 것이고, 반대로 임계치가 높을 때는 확실한 증거가 있지 않는 한 무죄 판결을 내릴 것입니다.

예를 들어, 한국 법원은 0.7, 미국 법원은 0.3의 임계치로 피고인을 판단한다고 합시다. 0.5의 혐의를 받는 사람은 임계치가 낮은 미국에서는 유죄, 비교적 임계치가 높은 한국에서는 무죄가 됩니다.

임계치가 굉장히 높다면 진짜 도둑임에도 놓치는 경우도 생길 겁니다. 반면, 억울한 사람은 굉장히 적어지겠죠. 이처럼 도둑을 많이 잡을수록 높아지는 재현율(recall)과 억울한 사람이 늘어날 수록 높아지는 위양성률(fall-out)은 일반적으로 양의 상관 관계를 가지는데, ROC(Receiver operating characteristics)는 저 관계를 그래프로 나타냅니다. ROC는 한국어로 수신자 조작 특성이라고 하는데, 이름만 어렵습니다.

MultiClass Classification

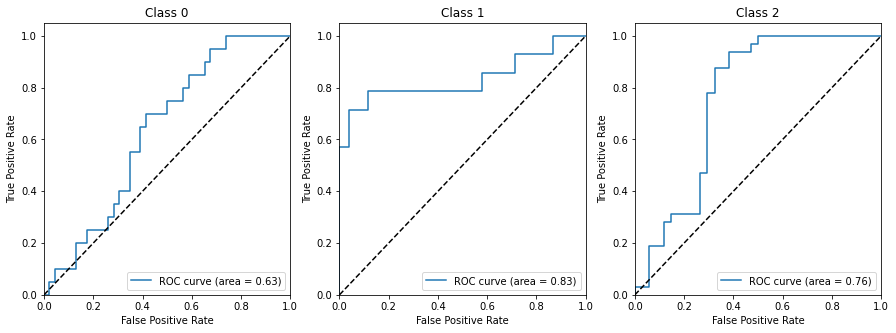
다중 분류 문제에서는 One-versus-Rest(OvR) 문제로 가정하고 (사람, 개, 고양이를 분류하는 문제일 경우에는 사람 vs 나머지, 개 vs 나머지, 고양이 vs 나머지) 각 클래스마다 하나씩 ROC커브를 그립니다.

AUC

ROC 곡선만으로는 어떤 수치를 나타내기 어렵습니다. 그래서 AUC를 사용하는데, AUC(Area Under the Curve)는 말그대로 ROC커브 아랫부분의 면적을 뜻합니다. 각 클래스별 AUC 값의 평균으로 계산합니다.

ROC 곡선 그래프에서 Threshold 값에따라 True Positive Rate(recall)과 False Positive Rate(fall-over)이 함께 증가하는 것을 확인할 수 있습니다. 사선으로 그어진 점선은 무작위로 추정(random guess)했을 때의 값으로, 저 선보다 ROC 커브가 아래에 위치해있다면 대충 찍은 것보다 못하다는 의미입니다. 그래서 AUC값은 0.5점을 0점으로 생각하면 됩니다. AUC가 1에 가까울수록, ROC 곡선이 사선에서 멀어질수록 좋은 모형입니다. 범인 한명 잡을 때 증가하는 억울한 사람이 적을 수록 좋은 거니까요.

사용 목적

그래서 결국 ROC를 왜 쓰냐하시면, recall, precision, fall-out등의 값은 threshold 값을 조작함에 따라 얼마든지 왜곡할 수 있기 때문에, threshold 값의 변화에 따라 변화하는 ROC 곡선의 면적을 계산함으로써 모델의 전반적인 성능을 확인할 때 사용합니다.

code

사이킷런으로는 아래처럼 ROC 곡선을 확인할 수 있습니다.

from sklearn.datasets import make_classification
from sklearn.metrics import roc_curve, auc, roc_auc_score

from sklearn.naive_bayes import GaussianNB
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import label_binarize
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

# make sample data
n_classes = 3
X, y = make_classification(n_samples=200, n_features=5,
                           n_informative=3, n_redundant=2
                           , n_clusters_per_class=2
                           , n_classes=n_classes
                           , weights=[0.3, 0.2, 0.5]
                           , random_state=99)

y = label_binarize(y, classes=[0,1,2])

# split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)

# classifier
clf = OneVsRestClassifier(GaussianNB())
clf.fit(X_train, y_train)
y_score = clf.predict_proba(X_test)
  # 나이브베이즈 모델은 predict_proba 메서드로 각 클래스별 probability를 구할 수 있습니다.

# ROC & AUC
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

# Plot of a ROC curve for a specific class
plt.figure(figsize=(15, 5))
for idx, i in enumerate(range(n_classes)):
    plt.subplot(131+idx)
    plt.plot(fpr[i], tpr[i], label='ROC curve (area = %0.2f)' % roc_auc[i])
    plt.plot([0, 1], [0, 1], 'k--')
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('Class %0.0f' % idx)
    plt.legend(loc="lower right")
plt.show()

print("roc_auc_score: ", roc_auc_score(y_test, y_score, multi_class='raise'))